Binary Search Tree

 

 

 

---

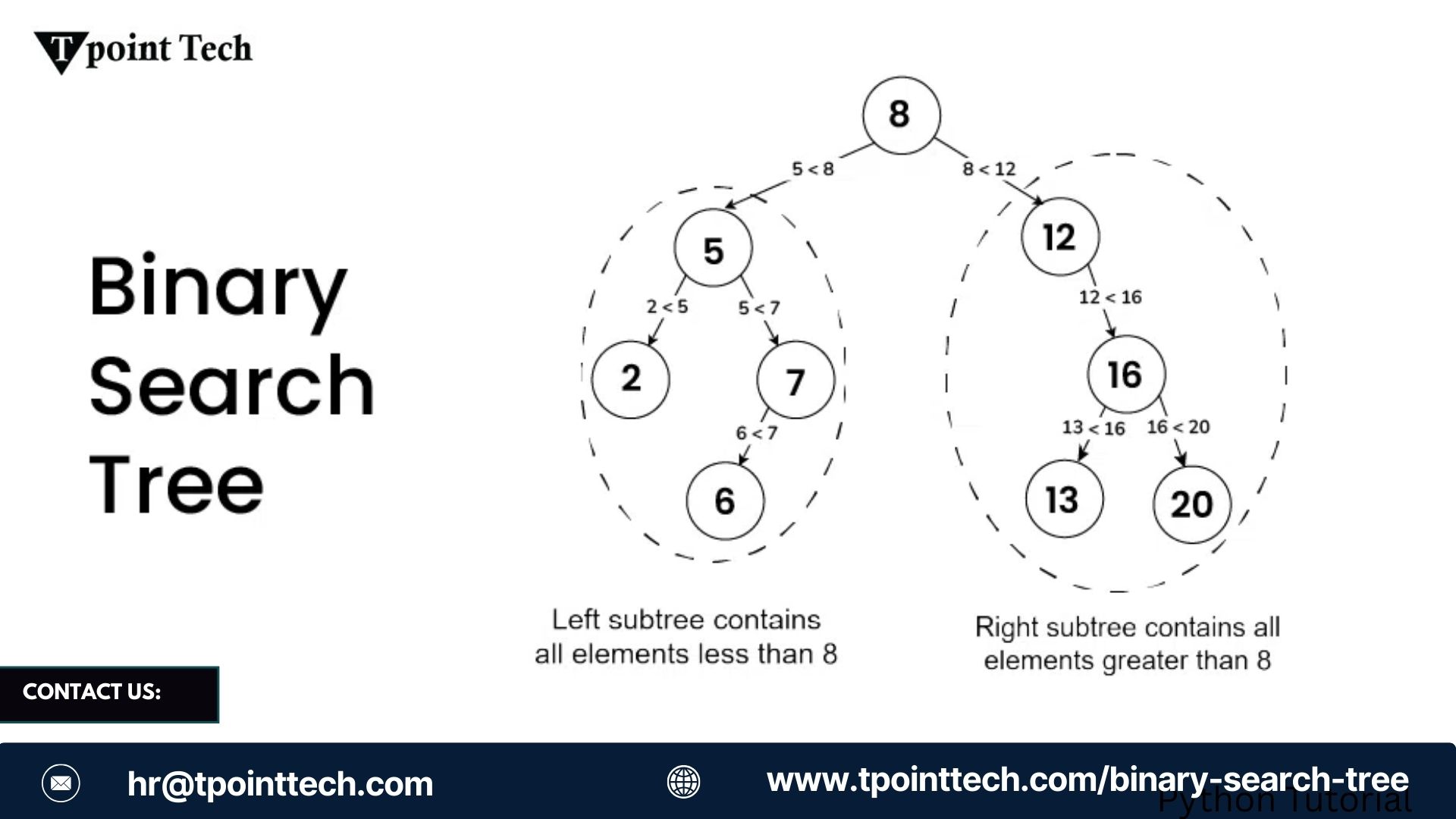
Introduction

A Binary Search Tree  (BST) is a specialized type of Binary Tree that maintains sorted order among its elements, making it extremely useful for operations like search, insertion, and deletion. In a BST, each node has at most two children: the left child, which contains values ​​less than the node, and the right child, which contains values ​​greater than the node. To effectively work with binary trees, especially for algorithms and data manipulation, understanding tree traversals is essential.

Tree traversal is the process of visiting every node in the tree exactly once in a specific order. The three primary types of depth-first traversal techniques are Inorder , Preorder , and Postorder . Each method follows a different sequence to process the nodes, and they serve different purposes depending on the application.

 

1. Inorder Traversal (Left → Root → Right)

In inorder traversal , we visit the left subtree first, then the root node, and finally the right subtree. This traversal is particularly important in a Binary Search Tree because it returns the node values ​​in sorted (ascending) order .

Algorithm:

Inorder(node):
    if node is not null:
        Inorder(node.left)
        Visit(node)
        Inorder(node.right)

Example:

Consider the following Binary Search Tree:

      8
     / \
    3   10
   / \    \
  1   6    14
     / \   /
    4   7 13

Inorder Traversal of this tree yields:
1, 3, 4, 6, 7, 8, 10, 13, 14

This output is in sorted order, illustrating why inorder traversal is commonly used to retrieve data from a BST.

 

2. Preorder Traversal (Root → Left → Right)

In preorder traversal , we visit the root node first, then traverse the left subtree, followed by the right subtree. This method is especially useful for creating a copy of the tree or saving its structure.

Algorith

Preorder(node):
    if node is not null:
        Visit(node)
        Preorder(node.left)
        Preorder(node.right)

Example:

Using the same Binary Search Tree:

Preorder Traversal yields:
8, 3, 1, 6, 4, 7, 10, 14, 13

Preorder traversal starts at the root and descends left before going right. This traversal can be used to serialize a binary tree into a file or memory.

 

3. Postorder Traversal (Left → Right → Root)

In postorder traversal , we traverse the left subtree first, then the right subtree, and finally the root node. This traversal is useful for deleting or freeing nodes , because it processes children parents before.

Algorithm:

Postorder(node):
    if node is not null:
        Postorder(node.left)
        Postorder(node.right)
        Visit(node)

Example:

Postorder Traversal yields:
1, 4, 7, 6, 3, 13, 14, 10, 8

In postorder traversal, the root is visited last, making it ideal for operations where the subtrees need to be handled before the parent node (eg, in memory deallocation).

 

Why Tree Traversals Matter

Understanding these traversal methods is crucial when working with any Binary Tree , not just BSTs. Each traversal technique solves different kinds of problems:

• Inorder : Best for retrieving sorted data from a Binary Search Tree .

• Preorder : Useful for copying a tree or converting it into a different format.

• Postorder : Ideal for deletion, evaluation of expressions, or memory cleanup.

For example, in expression trees (a specialized type of binary tree), these traversals correspond to different notations:

• Preorder → Prefix notation

• Inorder → Infix notation

• Postorder → Postfix notation

 

How to Implement Tree Traversals in Code (Python Example)

Here's how you can implement all three traversals using a simple Nodeclass:

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def inorder(node):
    if node:
        inorder(node.left)
        print(node.value, end=" ")
        inorder(node.right)

def preorder(node):
    if node:
        print(node.value, end=" ")
        preorder(node.left)
        preorder(node.right)

def postorder(node):
    if node:
        postorder(node.left)
        postorder(node.right)
        print(node.value, end=" ")

You can construct the Binary Search Tree manually and call these functions to see each traversal in action.

 

Conclusion

Understanding Binary Search Tree traversals is foundational for anyone learning data structures and algorithms. Whether you're performing searches, storing data efficiently, or managing system resources, knowing how to properly traverse a binary tree will make you a more effective programmer.  

By mastering inorder , preorder , and postorder traversals, you're not just learning how to walk through a tree—you're gaining powerful tools to solve real-world problems in software engineering, data processing, and algorithm design.